概要

かご型誘導電動機の定常状態の近似解は交流定常解析によっても求めることが可能であり，それを初期値として時間ステップ解析を行えば素早く定常解を求めることができることを"誘導電動機の解析"において示しました。交流定常解析は線形計算を行うため，適当な透磁率を与えて計算する必要があります。しかし，非線形性が強いとき，例えばソリッドロータの誘導電動機のような場合など，線形定常解析結果は定常解から大きく異なってしまう場合が多いと思われます。このような場合，交流定常解を初期値として時間ステップ解析を行っても定常解に達するには多大のステップを要してしまいます。"時間周期問題の定常解への高速収束"で紹介したように，同期回転機の場合，SD-EEC時間周期有限要素法は定常解を高速に得ることができます。しかし，この方法は固定子，回転子共に補正を行うため，誘導機のようなすべりがある場合は適用できません。
　誘導機ではステータ側である電機子電流の一周期とロータ側のすべり周期が一致しませんが，定常状態においては固定子のみで見た場合，電機子電流と磁場は近似的には半周期性（一周期の半分で符号が反転する）を有すると考えられます。回転子のロータバーとエンドリングに流れる電流の時定数は，固定子巻線の時定数に比べて小さいと考えられ，また回転子による非周期性も小さいとして，固定子のみの半周期の時間周期法を適用することが可能であると考えられます。そこでこの半周期性を利用し，固定子のみに時間周期法を適用する機能を開発しましたので報告します。

解説

適用する方法は簡易版時間周期法と呼ばれるもので，SD-EEC法では補正方程式を導出して補正量を求め，半周期もしくは一周期毎に補正を行うものですが，簡易版時間周期法の場合，半周期性に対して次の補正を行います。時間ステップ解析において，ある時点の方程式の解$x_0$ と半周期後の解 $x_1$に対して、補正量 $p$を次式で求めます。

$$ p=-\displaystyle\frac{x_0+x_1}{2}$$

x1←x1+pの補正を行い，その後の解析も半周期毎に補正を行っていくものです。補正のために方程式を解く必要が無く，簡便な方法ではありますが，SD-EEC時間周期法に比べ，定常解に達するまで補正回数をやや多く行う必要があるようです。

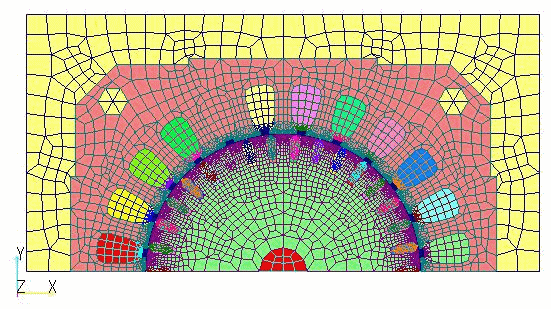
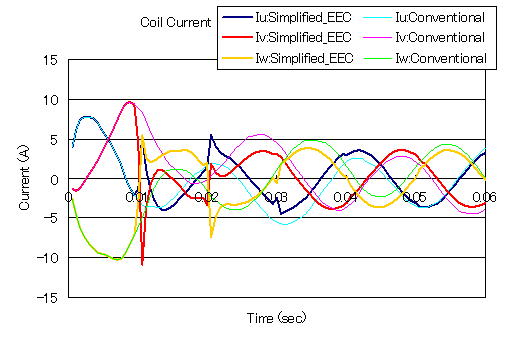
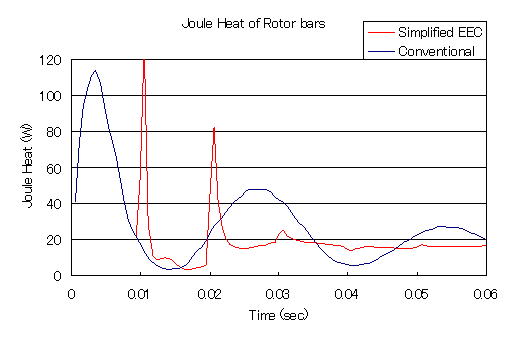
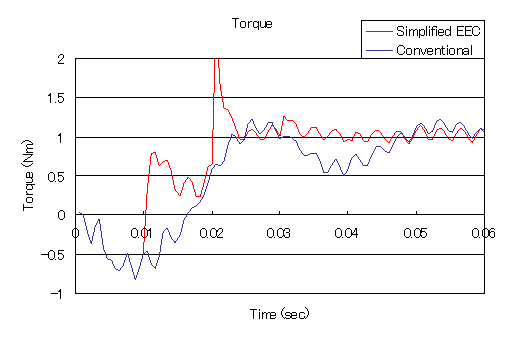
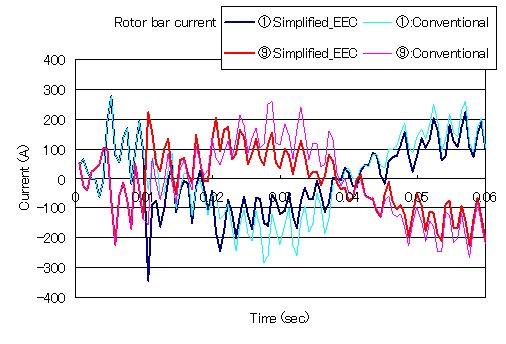
"誘導電動機の解析"で示したモデルに，ロータバーとエンドリングを等価回路としてモデル化した"かご型誘導機の二次元解析におけるロータバーとエンドリングの取り扱い"のモデルに簡易版時間周期法を適用した例を示します。ロータバーは別々のプロパティで作成し，それぞれSUFCURとして定義し，NETWORKによりSUFCURをエンドリングを模擬した仮想抵抗で接続した等価回路としています。上記方法の威力を見るため，初期値はゼロとして時間ステップ解析を行います。すべりは0.25で，時間ステップはやや粗いですが一周期34ステップとし，半周期である17ステップ目で補正を行っています。

通常の方法（Conventional）では過渡状態が次第に減衰していきますが，未だ定常には達していないのに対し，簡易版時間周期法（Simplified EEC）では，補正4回ほどでほぼ定常解が得られていることがわかります。

Fig.1 誘導電動機二次元メッシュモデル

Fig.2 回転数1125rpm
すべり S-0.25時の
固定子一次巻き線の電流変化

Fig.3 回転数1125rpm
すべりS=0.25時の
ロータバーの渦電流損失

Fig.4 回転数1125rpm
すべり S=0.25時の
回転子（半分）に働くトルク

Fig.5 回転数 1125rpm
すべり s=0.25時の
ロータバーの電流変化

これより，誘導機の定常解析に簡易版時間周期法が有効であることを示せたと思います。誘導機に適用する場合，先にも説明しましたように，この方法は固定子のみに補正を行う方法であり，固定子の電機子電流と磁場を半周期性であるとして解くものですが，半周期ごとにステータとロータバーの位置関係が必ずしも一致しないため，かなり定常解には近くなっていると思いますが厳密には定常解とはなりません。そのため，"周期的に印加される磁場に対する解の収束性"と同様の考え方で，最初は簡易版時間周期法で定常解に近いところまで計算し，それを初期値としてリスタート解析を行って定常解を得る，といったようにお使い頂ければと思います。

またSD-EEC法では，発電機や大型の界磁巻線型同期機でかご（短絡環）のロータバーをSUFCURとして定義して解析することはできませんが，上記誘導機の例で示しましたように，簡易時間周期法であれば解析することができます。