扁平・扁長要素の収束性の改善
- TOP >
- 機能別解析例・解析技術(一覧) >
- 扁平・扁長要素の収束性の改善
概要
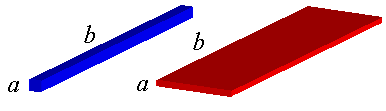
有限要素法においては、一般的にメッシュ内に偏平あるいは偏長な要素(Fig.1)が含まれますと行列の性質が悪くなり、ICCG法等の収束が遅くなります。EMSolutionにおきましては、極度に偏平な要素になる場合、二次元要素であるGAP要素に置き換えることができますが、三次元要素を使用したい場合が多くあります。例えば、プランジャーなどの運動解析を行う場合、ギャップが極度に小さくなるときがありますが、運動連成解析ではGAP要素は対応しておりません。また、二次元メッシュを積み上げにより三次元メッシュとする場合、空気領域に非常に偏平な要素ができてしまうことが多々あります。
そこで、EMSolutionにおきましては、このように非常に偏平あるいは偏長な要素が含まれる場合の収束性を改善する方法を導入しました。
解説
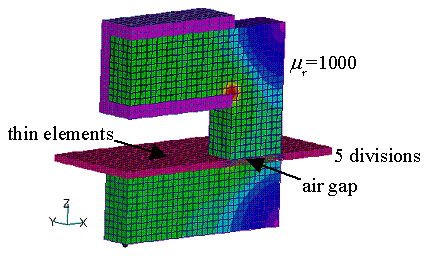
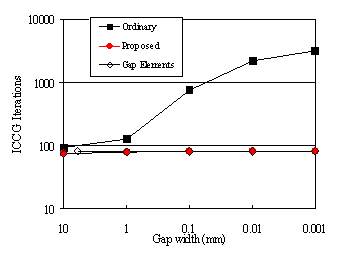
ここでは、解析例を通じてその効果を紹介します。まず、 "ギャップ要素を用いた解析"について示します。ここでは、Fig.2に示しますように、ギャップを三次元要素でモデル化し、変形(Deform)機能を使ってギャップ間隔を変化させる解析を行います。Fig.3にギャップ間隔に対するICCG法の収束回数を示します。本改善法を用いますと、三次元要素でギャップ間隔を1μmにしても収束回数が増大せず、非常に良い収束特性を示しています。
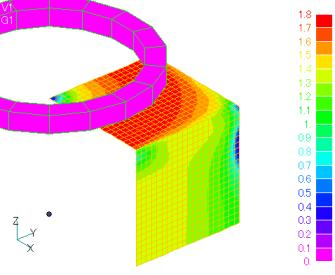
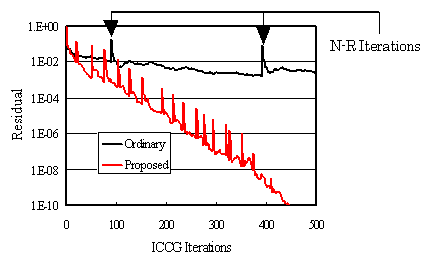
次に、電気学会検証用Box Shieldモデル(Fig.4)について示します。0.2m角の直方体シールド(厚さ0.01mm)に上下のコイルにより磁場を加えます。板厚方向に10分割しています。メッシュは二次元メッシュを三次元に積み上げて作成した直交格子を用いており、非常に偏平、偏長な要素が含まれます。特に外部の空気領域では、アスペクト比が2万に達する要素もあります。非線形静磁場解析を行い、鉄材(SS400)中の磁場は飽和磁界に達しています。Fig.5に収束過程を、TableⅠに要素数等の解析パラメータと計算時間を示します。本改善法を使用しない従来の方法に比べて、ニュートン・ラフソン法の反復回数はそれ程変わりませんが、ICCG法の反復回数が約1/24と非常に少なくなっています。これにより、従来34分かかっていたものが、4分足らずと9倍以上高速に求解できています。なお、本改善法では、若干未知数の数と行列非ゼロ要素の数が多くなり、使用メモリは増大します。
Table I. 解析パラメータと計算時間
| Ordinary | Proposed | |
|---|---|---|
| Number of elements | 125,000 | |
| Number of nodes | 132,651 | |
| Number of unknowns | 365,050 | 374,370 |
| Number of Non-zeros | 6,016,122 | 7,606,586 |
| N-R iterations | 25 | 19 |
| Total ICCG iterations | 13,410 | 546 |
| CPU time (s) | 2,056.3 | 223.1 |
これらより、本改善法の有用性を示せたと思います。本改善法は、特に空気中の偏平・偏長要素に対して効果があるようです。渦電流の表皮層に適用することも考えられますが、あまり効果は無いようです。6面体、3角柱要素に対して適用できます。もちろん本機能を使用した場合と使用しない場合で計算結果に差異はありません。本機能はEMSolution ver10.1.1より使用可能となっています。
この先は会員の方のみご覧いただけます。
機能別解析例
収束特性改善、高速化手法
- INIT OPTIONの効果
- 非線形オプション比較
- 収束条件と解析精度
- 扁平四面体要素の問題点とその解決法
- 節点二次辺一次要素
- 六面体要素と四面体要素の接合
- 扁平・扁長要素の収束性の改善
- 周期的に印加される磁場に対する解の収束性
- 時間周期問題の定常解への高速収束
- 簡易版時間周期法による誘導電動機の定常解析
- 多相交流簡易EEC法による回転機の定常解析
- 時間周期条件を利用したdq軸座標系でのTP-EEC法(dq-TP-EEC法)
- 変形ポテンシャル領域に配置する外部磁場電流ソースのICCG法収束性に対する影響
- OpenMPによる並列計算機能
- 収束条件変更のリスタート解析
- 定常周期性を利用した反復計算時の初期値設定
キーワード
©2020 Science Solutions International Laboratory, Inc.
All Rights reserved.