概要

これまで，定常周期解の高速手法として，TP-EEC法“時間周期問題の定常解への高速収束”や簡易TP-EEC法“簡易版時間周期法による誘導電動機の定常解析”，多相交流簡易TP-EEC法“多相交流簡易EEC法による回転機の定常解析”を導入してきました。これらの手法は時間周期性を利用して補正する方法で，補正方程式を解いて得られた補正量を，電気角一周期や半周期（TP-EEC法。簡易TP-EEC法は半周期のみ），多相交流簡易TP-EEC法は多相交流条件の半周期で補正する方法です。例えば三相交流簡易TP-EEC法では，三相交流の半周期である1/6周期での補正が可能です。
多相交流簡易TP-EEC法の考え方を三相交流に限定し，補正方程式をdq軸座標系で表現して補正量を直流量とすることで，任意の補正周期で補正することができるdq-TP-EEC法を開発しました。三相PMモータでの検証解析では素早く定常解に収束することを示せましたので，紹介いたします。

解説

dq軸座標系は，三相交流（5相や6相交流でも可能）を静止座標系から回転座標系に座標変換して，基本波成分を直流成分として表現でき，モータ制御やモータ設計で使用されているものです。三相交流の変換行列は次式で表されます。なお，次式では零相成分も示しています。

$${ \begin{Bmatrix} x_{d} \\ x_{q} \\ x_{0} \\ \end{Bmatrix} = D \begin{Bmatrix} x_{a} \\ x_{b} \\ -x_{c} \\ \end{Bmatrix} ・・・（１）}$$

$${ D = \begin{bmatrix} cosθ & cos(θ-\frac{2}{3}\pi) & cos(θ+\frac{2}{3}\pi) \\ -sinθ & -sin(θ-\frac{2}{3}\pi) & -sin(θ+\frac{2}{3}\pi) \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \end{bmatrix} ・・・（２）}$$

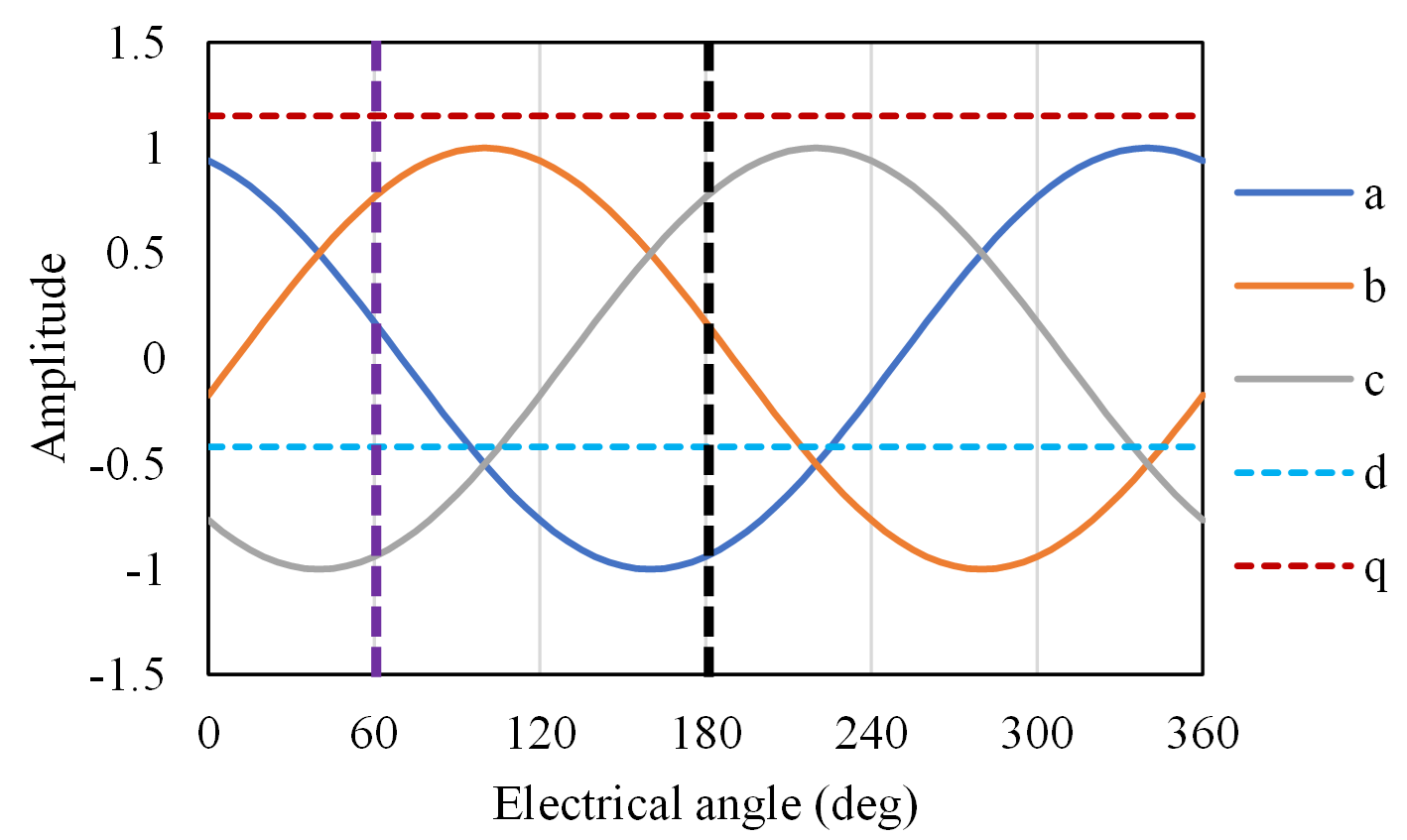
ここで，$\theta$は電気角です。Y結線を採用すると，三相平衡条件$I_a$ + $I_b$ + $I_c$ = 0より，変換後の零相成分は0となるため無視でき，dq軸成分を考えればよいことになります。dq変換のイメージをFig.1に示します。

Fig.1 三相交流とdq軸電流
（黒点線が半周期，紫点線が1/6周期を示している）

基本波成分に対する同期回転速度におけるdq変換後の物理量は直流成分のみとなるため，一周期よりも小さい任意の時間区間に対して時間周期境界条件を適用することが考えられます。$n$ステップの時間区間に対する一周期性の時間周期条件は，次式で表されます。

$${ \begin{Bmatrix} x_{d}^{0} \\ x_{q}^{0} \\ \end{Bmatrix} = \begin{Bmatrix} x_{d}^{n} \\ x_{q}^{n} \\ \end{Bmatrix} ・・・（３）}$$

通常のTP-EEC法の補助方程式を三相座標系で表記して，dq座標変換を施したのち，一周期性の圃場方程式で表すことを考えます。補正方程式を簡易TP-EEC法と同様に表すと，次式となります。

$${ \left\{ \begin{array}{ll} P_{d} = \frac{1}{n \omega \Delta t}(x_{q}^{n}-x_{q}^{0}) & \\ P_{d} = \frac{1}{n \omega \Delta t}(x_{d}^{n}-x_{d}^{0}) & \end{array} \right. ・・・（４）}$$

１. 検証モデル

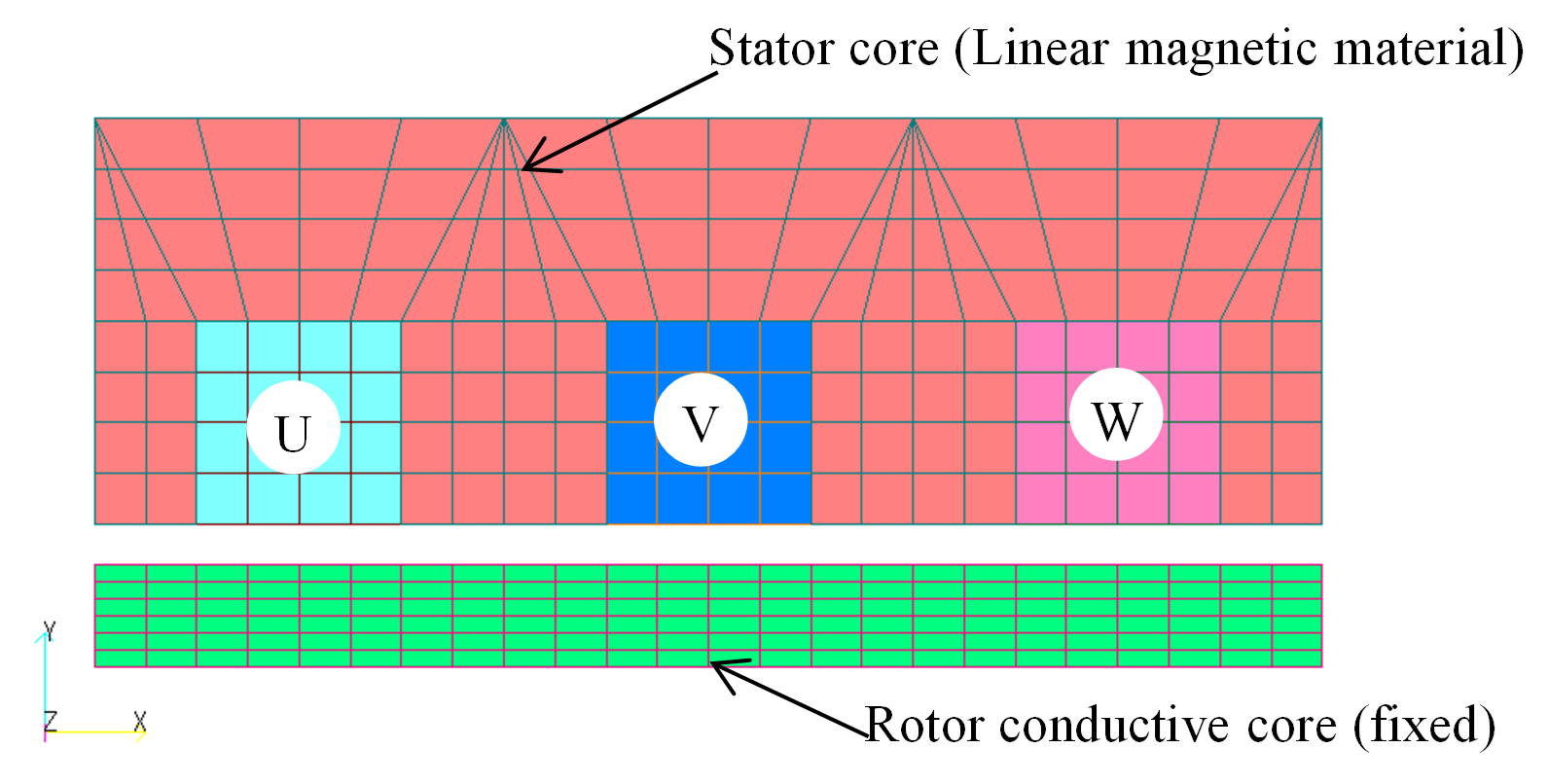
まず簡単な場合として，“多相交流簡易EEC法による回転機の定常解析”でも用いた簡易リニアモータモデルでその効果を検証します。Fig.2に三相コイルを模擬した検証モデルを示します。ステータとして三相コイルとその周りに線形磁性体を配置し，ロータは非磁性導体としている。三相正弦波電圧をコイルに印加し，コイル電流結果より補正効果を確認します。

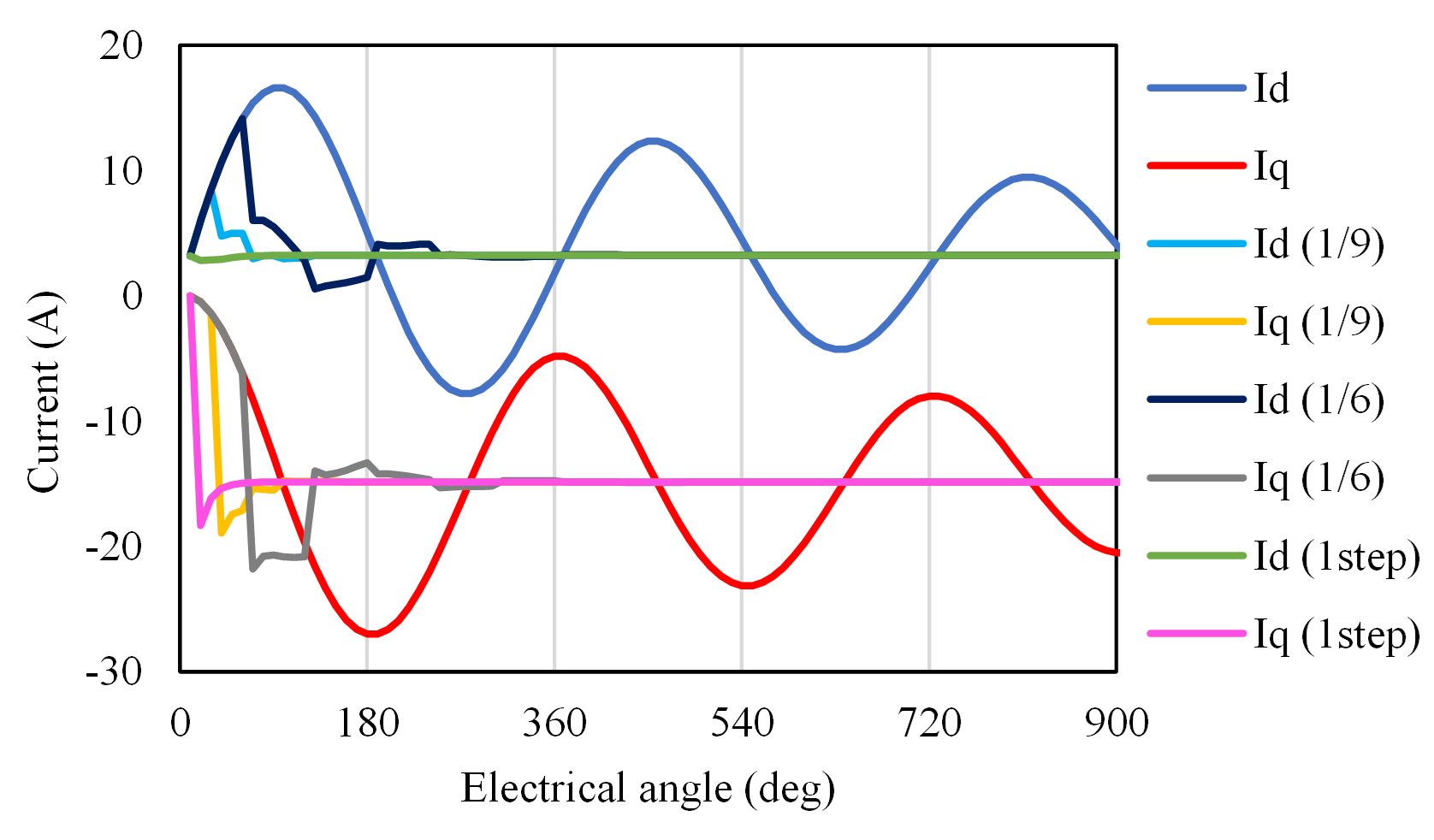
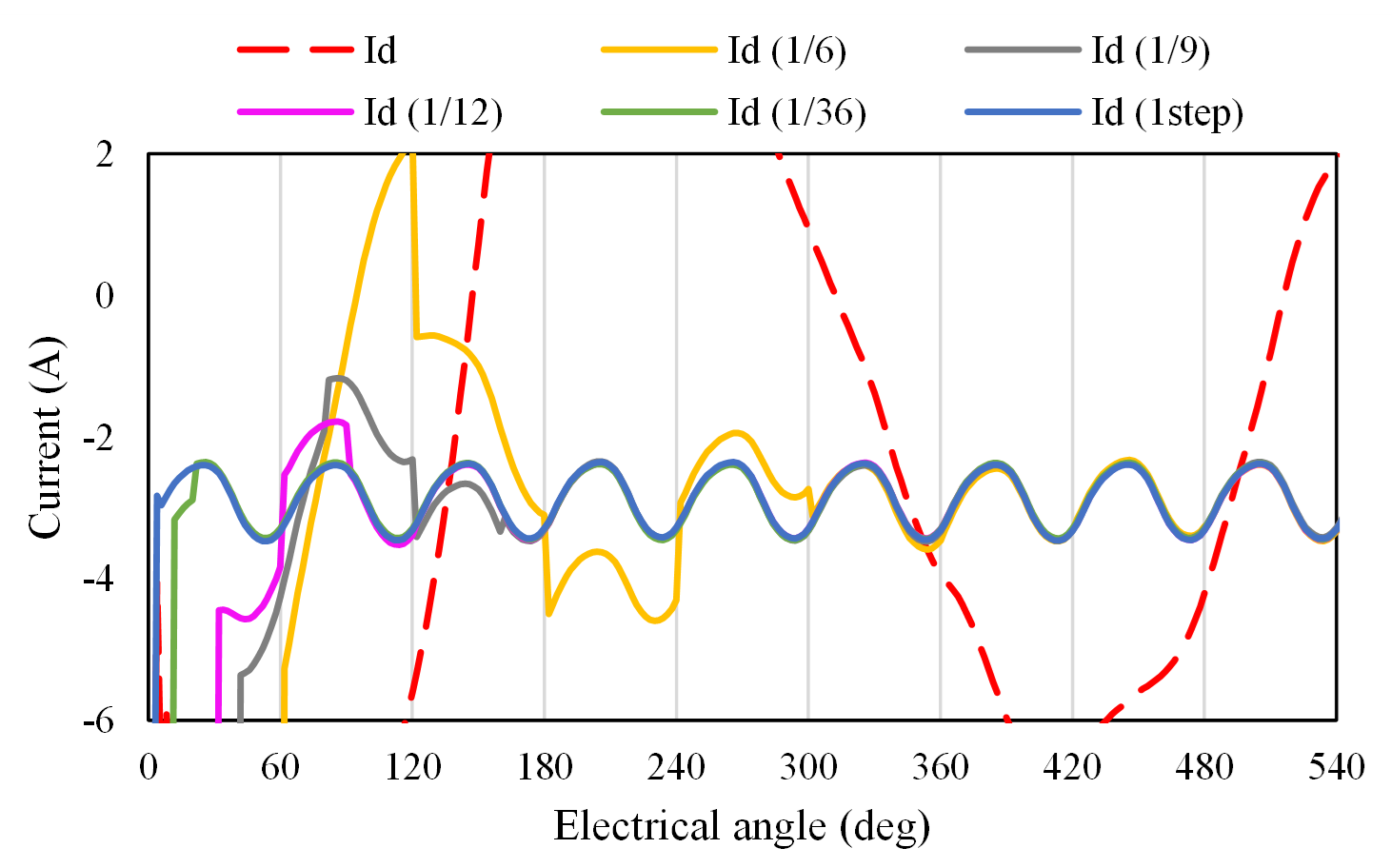
Fig.3に計算結果として，コイル電流波形を示します。なお，今回のモデルはスロットによる空間高調波の影響が小さいものです。$I_{d}$, $I_{q}$は補正していない場合の電流波形で，コイルの時定数でゆっくりですが徐々に定常値に近づいて行っています。これに対し，三相交流の半周期である1/6周期，それよりも短い1/9周期では，補正効果によって素早く定常値（一定値）になっていることがわかります。さらに1ステップ補正（1step）でもすぐに定常値になっていることがわかります。

2.IPMモータモデル

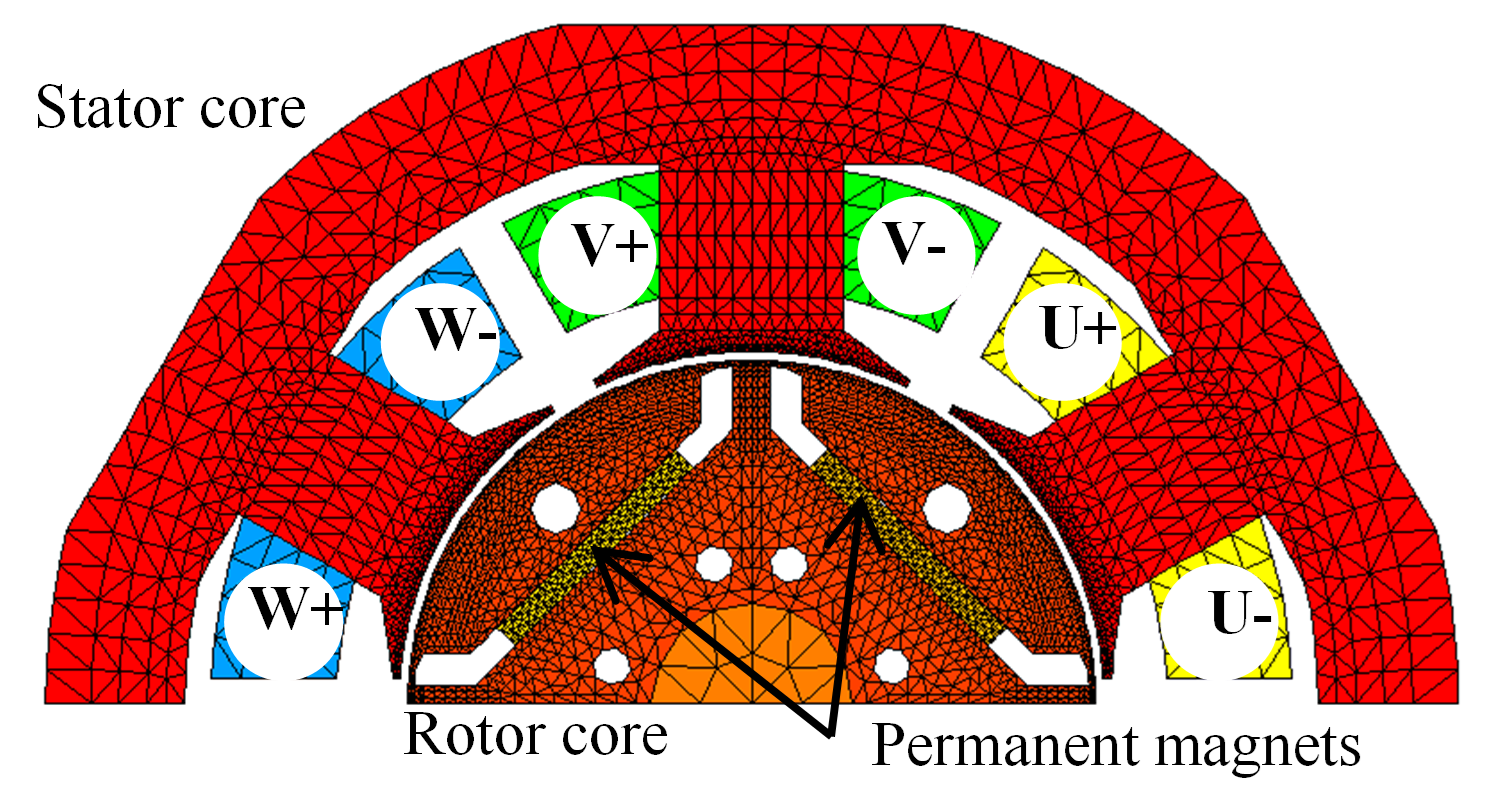
次に，Fig.4に示す電気学会ベンチマークモデル「D1モデル」を使用した検証結果を示します。一般的にモータコイルの時定数は大きいため，電圧源解析の場合はTP-EEC法の適用が非常に有効です。

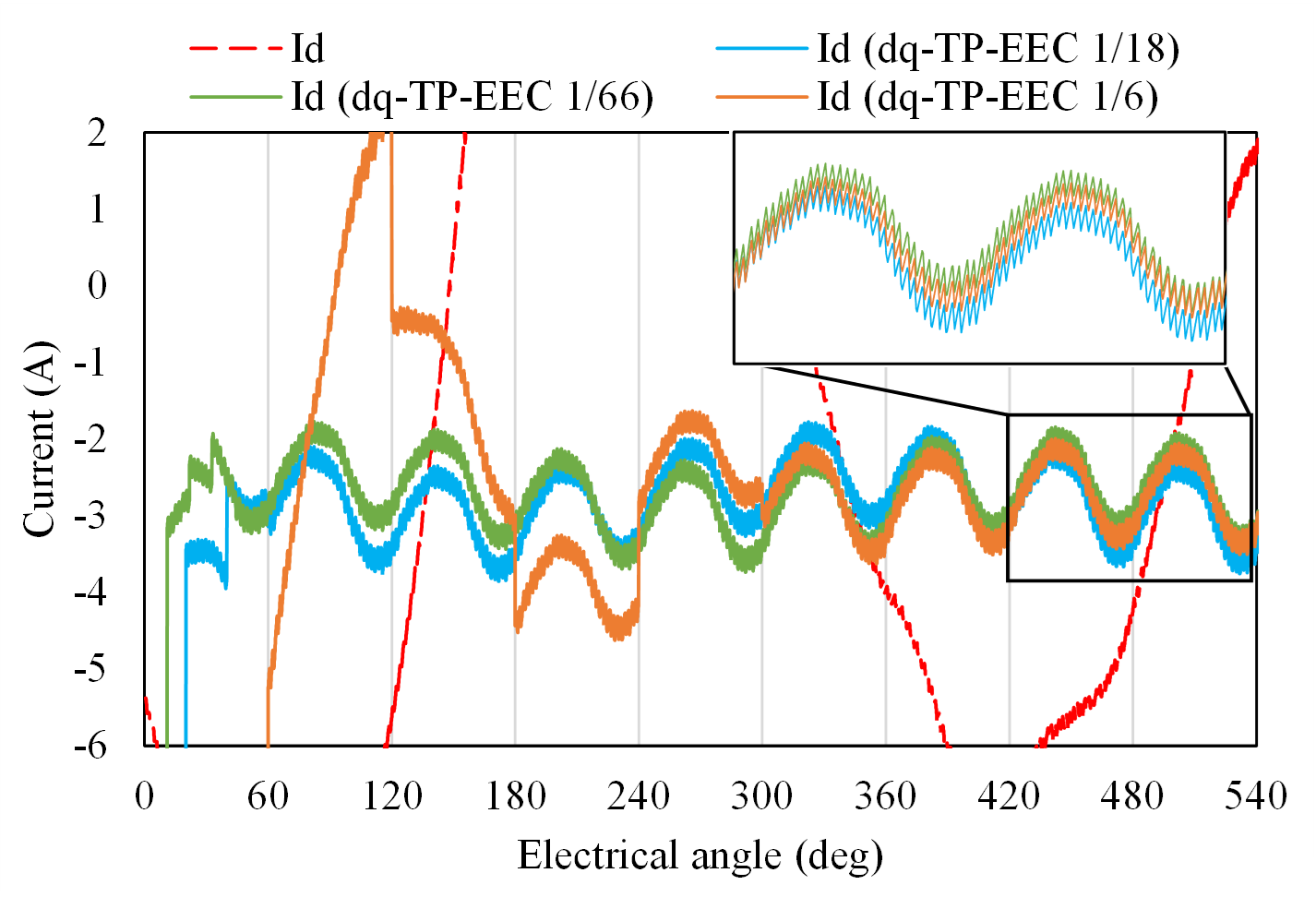
正弦波電圧源解析した結果をFig.5(a)に，PWM電圧源解析した結果をFig.5(b)に示します。正弦波電圧源解析だと，1step補正でも定常に達していることから，dq-TP-EEC法の補正効果が強力であることがわかります。PWM電圧源解析だと，1/6周期補正では厳密に定常に達しています。一方，それ以外の小さい補正周期（1/18. 1/66）は補正効果によって定常値に近づきますが，高調波が残ってしまうようで厳密には定常状態には近づかないようです。しかしながら，補正しない場合に比べて素早く定常状態に近づけることができ，さらにdq-TP-EEC法の補正区間をうまく組み合わせることで，素早く定常に達することができると予想されます。

以上，簡単ではありますが，dq-TP-EEC法による定常解の高速求解について紹介いたしました。モータ解析での計算時間の短縮にご使用いただければと思います。理論的な説明と詳しい考察は，下記論文にまとめてありますので，ご興味のある方はご参照いただければと思います。

参考文献

Hiroyuki Kaimori, Yasuhito Takahashi, Shinji Wakao, :
“Steady-State Analysis of Electric Machines Using the TP-EEC Method Based on Time-Periodic Conditions in a Rotational Reference Frame”,
IEEJ Journal of Industry Applications, DOI