概要

周波数が高い場合や、導電率、透磁率が高い場合、渦電流の表皮の厚さが解析する対象より非常に小さくなる場合があります。この場合、物性が線形の場合は表 面インピーダンス法が使用できます。これにより、表皮厚さ内のメッシュ分割が不要となり、計算速度や精度を向上させることができます。

解説

"渦電流を含む解析"では導体が導電率$\sigma=5.0×10^7 S/m$、比透磁率1としました。
周波数が50Hzとしますと表皮の厚さdは

$$d=\sqrt{\frac{2}{\mu \sigma \omega}}$$

から10mmとなります。
導体寸法を同じとしますと寸法100mmと比べて1/10となります。これに対して表面インピーダンス法を適用してみます。

表面インピーダンス法を使用する場合は、Fig.1の様に導体の表面に外向き（空気領域に向かって）に面を定義します。 対称面には不要です。 導体内部からは要素を除きます。 二次元からの拡張は、2D_to_3Dにより行います。 メッシュファイルpre_geom2D.neuには銅表面を表す線要素が定義されています。 inputファイルで面要素の物性を入力し、実行します。

表面インピーダンス法では、熱発熱は1周期平均で出力します。 このため、トータルの熱発熱やその分布を出力するときには、サンプルのinput2でリスタートして下さい。

出力ファイルoutputの一部をList.1に示します。 今回の場合、表面インピーダンス要素からの発熱量が出力されます。 電圧および発熱は表面インピーダンスを使わない通常のものとかなり良い一致を示しています。

Fig.1とFig.2にインピーダンス表面における渦電流分布を示します。 この分布は、面電流分布を示し、表皮厚さ方向に積分した電流量です（surface_currentファイル）。 Fig.3に平均表面発熱密度分布を示します（surface_heatファイル）。 表面インピーダンス法を使わない場合と使った場合を比べますと、角付近の分布が大きく違っていることがわかります。 一般的に、表面インピーダンス法は角付近で精度が悪くなります。

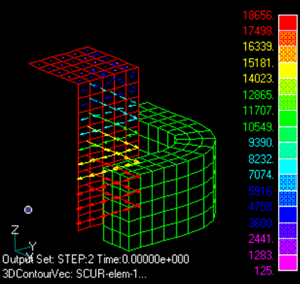
Fig.1　0度
インピーダンス表面の電流密度分布

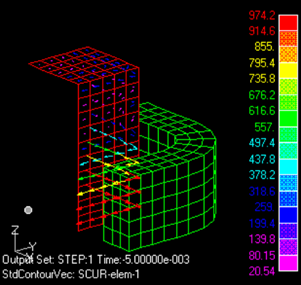
Fig.2　-90度
インピーダンス表面の電流密度分布

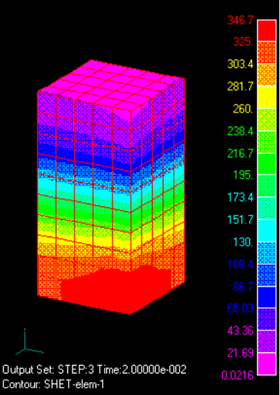
Fig.3　表面発熱密度分布$（W/m^2）$

List.1 ファイル　output

****************************************************************************** * Step No.1 Time -5.000e-003 sec * ****************************************************************************** *** Sources ********************************************************** ID No. Amplitude（Current） Voltage Flux 1 6.12303e-017 3.67318e+002 -8.26801e-002 *** Power Sources **************************************************** ID No. Current Voltage 1 6.12303e-017 3.67318e+002 ****************************************************************************** * Step No.2 Time 0.000e+000 sec * ****************************************************************************** *** Sources ********************************************************** ID No. Amplitude（Current） Voltage Flux 1 1.00000e+000 7.18802e+001 1.16921e+000 *** Power Sources **************************************************** ID No. Current Voltage 1 1.00000e+000 7.18802e+001 ****************************************************************************** * Total Joule heatin loss ( 1 cycle average ) in impedance_elements regions * ****************************************************************************** MAT No. Q （W） 101 1.6234e+000 ← 表面インピーダンス 面平均 全発熱 Total 1.6234e+000