辺要素有限要素法は、1980年代から広まった比較的新しい解析技術ですが、その利点が認識され広く用いられるようになり、EMSolutionにおいても採用しています。$A$-$\phi$法辺要素法では、$A$に対し辺要素形状関数を適用します。従来の節点要素法では各節点に$A$のベクトル3成分を未知数として割り振ってきましたが、辺要素法では各辺に$A$の線積分量を割り当てます。辺要素形状関数の特徴は要素境界で接線成分のみの連続性が有るのみで、法線方向の連続性は仮定しません。
 
　辺要素の導入により、それまで困難であったことや不明確であったことが解決されました。高周波解析でのスプリアス解が出なくなったことはよく知られていますが^[20]、低周波領域でも多くのことが解決されました。
 
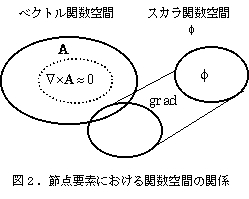
　まず、ゲージ問題の解決があります。節点要素法ではゲージ固定のためにペナルティ法等によりクーロンゲージを課すことが行われましたが、その必要性やペナルティの重みが不明確なものでした。境界条件を適当に入れれば解けてしまう場合も有りました^[21,22]。節点法における問題点は、その使用される有限要素関数空間の中の非回転場（回転(rotation)がゼロの関数空間）が不明確で(図2)、これを除くためにはいろいろな工夫が必要だった様に思われます。
 
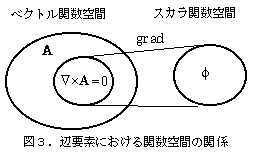
　辺要素の導入により、ゲージ問題は一気に解決されました^[13]。まず、節点要素では離散化された関数空間の中でゲージ変換は困難でしたが、辺要素関数空間の中では連続場と同様に変換が可能になりま した。ゲージ不定性は、ゲージ変換可能性があって意味を持ちます。$A$-$\phi$法おいては、ベクトル場$A$とスカラ場$\phi$のゲージ変換が自由にできることになりました。離散化された辺要素関数空間の中では、ベクトル場の中の非回転場はスカラ場の勾配(gradient)で表され、スカラ場の勾配がベクトル場に含まれるように構成することができます(図3)。このことにより、非回転場を明確に分離することが可能になりました。このことは、$E=-\dot{A}-\nabla\phi$とポテンシャル表示した場合、元々$\dot{A}$と$\nabla\phi$は同じ一つのものを表現していることを意味し、相互に入れ替えられることを可能にしました。

 
　上に述べたように離散化関数空間の中でもゲージ変換が可能で有ることは、何らかのゲージ変換を課さなければ、不定性が方程式の中に残ることを意味します。ICCG法により不定方程式を解くことについては後で述べますが、ここではゲージ固定について述べます。
 
　ゲージ固定の方法として、一つは木構造(Tree, Co-tree)による固定方法があります^[13,23]。これは、有限要素メッシュ内の辺を回路網解析の手法で分解することによります。Treeとは、閉ループを構成しない最大数の辺の集合であり、Co-treeはそれを加えると閉ループができてしまう辺の集合と言えます。その分解の仕方は一意的では有りませんが、それぞれの数は決まっています。このように分解し、通常Tree辺の自由度はゼロとし、変数から除きます。この方法は、明確に不定性を除くことができ、理論的には美しいのですが、共約勾配法の収束が(極度に)遅くなることが知られています^[24]。

　ゲージ固定のもう一つのとして、辺要素でもクーロンゲージを、ラグランジの未定常数法の形で課す方法が有ります^[25]。そこでは、クーロンゲージ（$\nabla \cdot A$=0）の弱形式を条件として課します。この手法は、物理的にも意味のあるゲージを課すことで、ポテンシャルの意味が分かりやすいものにはなりますが、解法としては、未定常数が加わり未知数が多くなること、行列の正値性が無く解きにくいもの（と思われる）になり、不利と思われます。そのようにしなくても、クーロンゲージを満たしていない解から、ゲージ変換によりクーロンゲージを満たす解を求めることが可能です^[26]。
 
　導体部に対しては、$φ$=0のゲージを課すことができます^[13]。これだけでは非導体部の不定性は残されますが、ICCG法により解くことができ、通常$A$法と呼ばれています。このように、種々ゲージ固定のやり方はあり、求まったポテンシャルはそれぞれ異なりますが、それらは相互にゲージ変換できることが示され、物理的に意味のある電場や磁場を計算しますと、全く同じ結果となります。
 
　EMSolutionでは、$φ$=0のゲージや木構造によるゲージ条件を入れられるようにしています。ただ、木構造によるゲージはICCG法の収束が遅いことが理論的にも示され^[28]、また実際的にも非常に計算時間がかかり、実用性はあまりありません。また、ゲージは未知数は少なくなるのですが、やはり収束が遅くなります。特に、低周波の渦電流解析では$φ$を変数とすることは必須のものと思われます。
 
　辺要素により、容易でわかりやすくなったものの一つとして、境界条件が有ります。電磁場解析での代表的な境界条件として、電気壁条件（$B_n$=0）と磁気壁条件（$H_t$=0）が有りますが、$A$-$\phi$法辺要素では電気壁に対しその面上の辺の自由度をゼロ固定条件、磁気壁では自由にすれば充分です。節点要素ではこうはいかず、傾い境界面では三成分を考える必要がありますし、角点では話は複雑になります。
 
　辺要素形状関数では、要素境界でベクトルの法線成分が連続にはなりません。例えばベクトルポテンシャル$A$を辺要素で表現した場合、上の不連続性が電場$E$に現れます。ポテンシャルが不連続になることが嫌われることがありますが、この方が合理的です。例えば、$A$法で渦電流を計算し、導電率に不連続性が有ったとします。この時、渦電流の法線成分は連続になるはずで、$A$の法線方向成分は不連続となる必要が有ります。$H$法（これは$T$-$\Omega$法でのゲージ条件を課したものです。）においても同様に、磁束法線成分の連続性が同じ話となります。節点要素の法線成分連続な関数を使いますと、この様な不連続面ではうまく行きません^[22]。
 
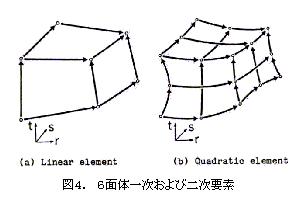
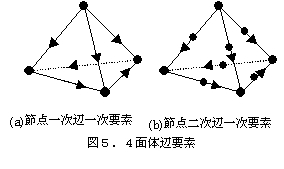
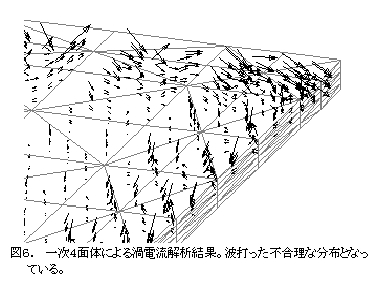
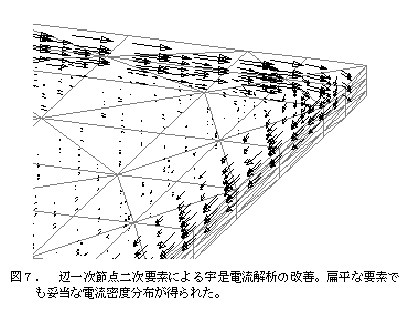
　EMSolutionでは、辺要素種としては、4面体(4辺Nedelec一次)、三角柱（9辺）、6面体(12辺)の一次要素、セレンディピティ族20節点6面体^[17]に対応する二次6面体要素(36辺)（図４）を用意しています。最近、表皮効果の大きい渦電流解析で一次４面体要素を使用すると、渦電流密度分布が滑らかにならないことが解り、一次辺要素に二次節点要素関数を加えたものを考案し、扁平な４面体要素でも妥当な解が 出ることを示しました^[2]（図５，６，７）。