概要

特にスロット構造を持つ回転機では，磁束密度等は時間高調波と空間高調波を持つことが知られています。時間高調波を簡単に説明すると，電源から入力される基本波に高調波が重畳している状態，例えばPWM電圧駆動により電流に高調波が重畳する場合に見られます。空間高調波は回転機内部に空間的に分布するもので，基本波の空間分布に対し高次の空間分布をするものです。例えば4極機の場合，基本波磁束密度は空間的に180度で一周期の分布で，3次の空間高調波が存在した場合，基本波の空間分布に対し3周期の分布をします。

周波数分解を利用した回転機の電磁加振力を評価する場合の手法として，電気角一周期分のギャップ磁束密度を用いて電磁力を算出し，空間と時間でフーリエ級数展開することで空間次数と時間次数の電磁力強度を知ることができます。これは音・振動解析で用いられている方法でもあり，ステータ等の構造物の固有振動数と共振していないかを確認することができます。

また，周波数分解された次数ごとの磁束密度分布や渦電流分布を考察することで，よりよい形状等を知る手掛かりとなると思われます。文献(1)ではIPMモータに対して周波数分解された次数ごとの磁束密度分布結果を示しておりますが，EMSolutionのすべての機能で周波数分解機能に対応できておらず，公開を見送っておりましたが，この度，制限付きではありますがリリースすることとしました。未対応の機能は以下となります。

• COIL_MOTION（未対応）
• メッシュ変形DEFORMの変形領域 変形領域も次数別の結果は出力されますが，要素変形が考慮されておりません

本機能は通常の過渡解析を実行後のポスト処理機能としてご使用いただけます。EMSolution内部で磁気ベクトルポテンシャル$A$と電気スカラーポテンシャル$\phi$をフーリエ級数展開し，次数ごとに磁束密度や渦電流密度を出力しています。

解説

以下に，IPMモータを用いた周波数分解例を示します。文献(1)で使用した電気学会ベンチマークモータ“Dモデル（分布巻）”と“D1モデル（集中巻）”における次数別の磁束密度分布を示します。図1に解析メッシュを示します。両機は体格，寸法がほぼ同じで図中(a)が4極24スロットのDモデル，(b)が4極6スロットのD1モデルです。計算条件はDモデルが定格である3Arms，$\beta$=25degで，D1モデルは定格に近い3Arms，$\beta$=20degです。

(a) Dモデル(分布巻)

(b) D1モデル(集中巻)

図1　解析メッシュ図

一般に平均トルクに寄与する次数成分は基本波成分が最も大きく，電機子巻線を持つステータでは時間次数も空間次数も基本波1次となります。同期モータではロータは基本波による回転磁束に同期しているため，ロータの回転座標から見た場合，時間次数も空間次数も基本波次数は0次となります。ステータには，自身の回転磁界とロータによる回転磁界の和によるものが現れますが，ロータには，自身の回転磁界は無く，ステータによる回転磁界のみが現れます。そのため，ステータの5，7次は，ロータの6次に，ステータの11，13次は回転子の12次に相当することになります。そのため，周波数分解をすることで評価項目に対する次数ごとの寄与度をみることができます。

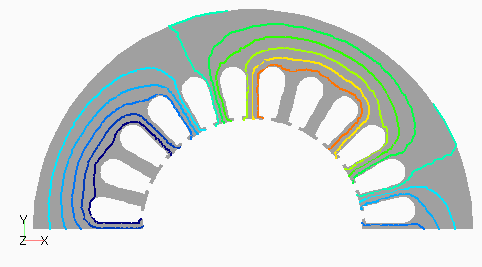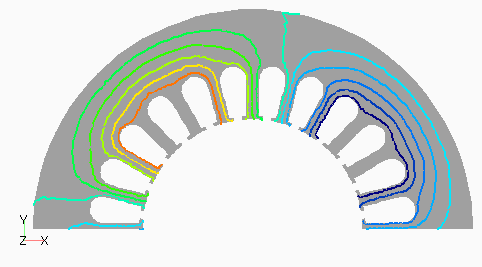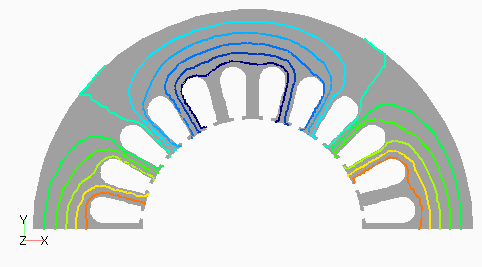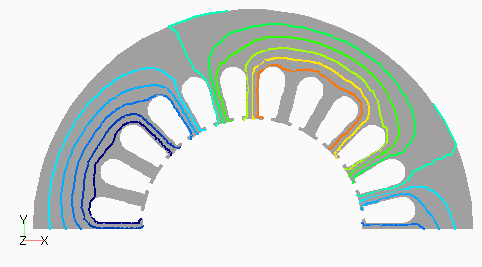
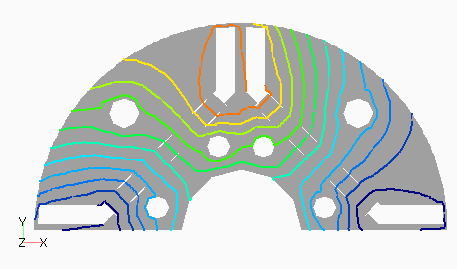
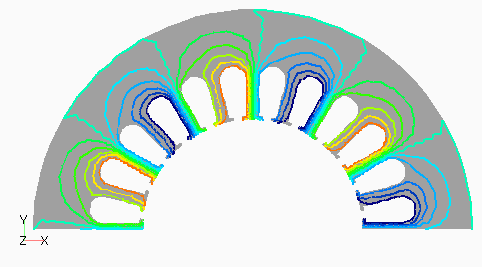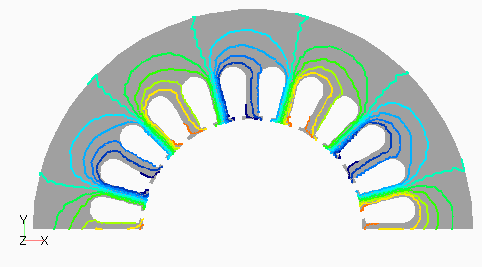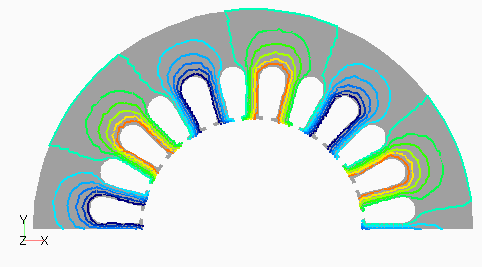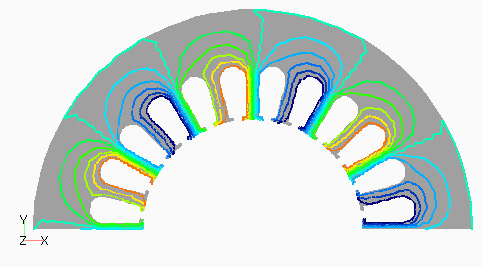
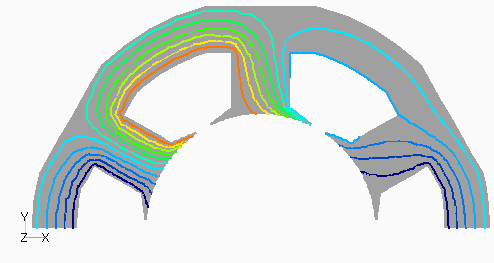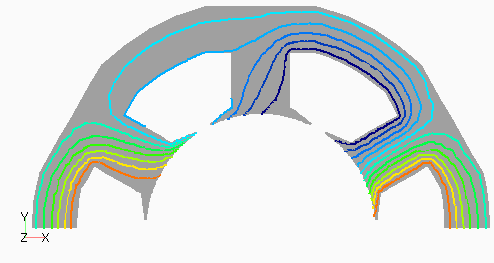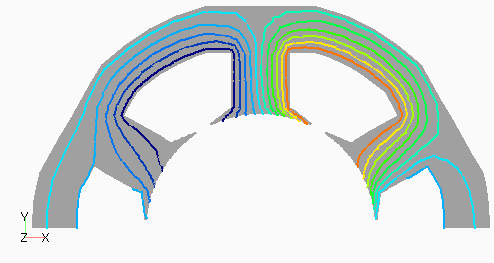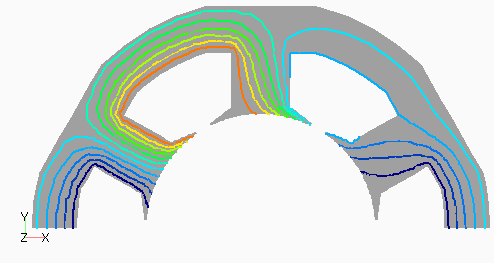
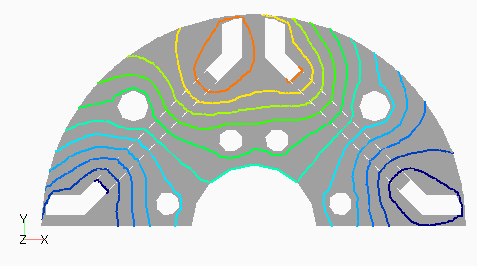
Dモデルの次数別の磁束分布として，図2(a) にステータ1次，(b)にロータ0次を，図3(a)にステータ3次，(b)にロータ12次を示します。ステータ1次とロータ0次は周波数分解しない分布でも見られる，主磁束の流れを表しています。ステータ3次は集中巻であるD1モデルとの比較用ですが，分布巻であるため空間的に三次の分布がきれいに出ていることがわかります。ロータ12次はスロット高調波に起因するもので，ロータ表面に空間的にもほぼ12次の分布となっています。

なお，磁束分布はステータは静止座標系，ロータはロータに固定した座標系である回転座標系で出力したものです。

(a) ステータ1次

(b) ロータ0次

図2　Dモデル　磁束分布

(a) ステータ3次

(b) ロータ12次

図3　Dモデル　磁束分布2

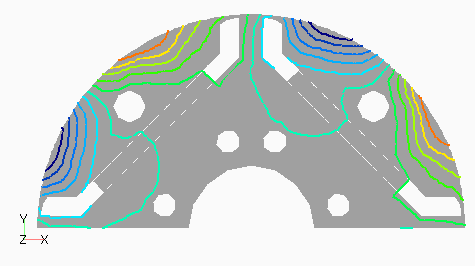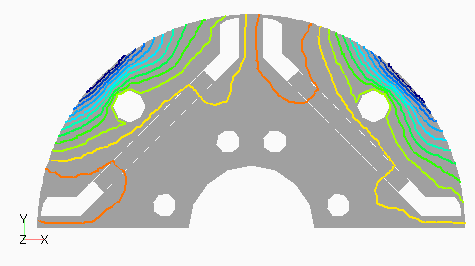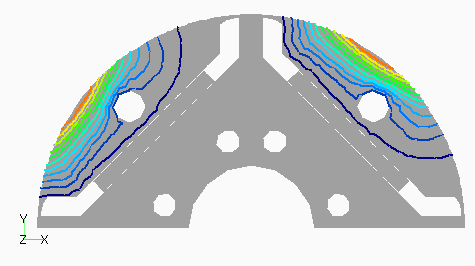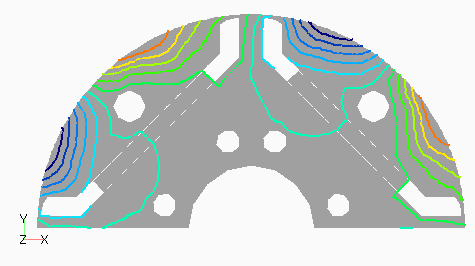
次に，D1モデルの次数別の磁束分布として，図4(a) にステータ1次，(b)にロータ0次を，図5(a)にステータ3次，(b)にロータ12次を示します。ステータ1次の基本波分布はスロット数が奇数であるためDモデルのようにきれいな分布となっていないようです。ステータ3次はスロット数と一致するため，空間的にも3次の分布が見られます。ロータ3次は磁極数が2次であるためか3次ではなく2次の分布になっているように見えます。

これらより，同じ4極機でも分布巻と集中巻の違いにより，現れる次数も異なり，分布も異なってくることがわかります。

(a) ステータ1次

(b) ロータ0次

図4　D1モデル　磁束分布

(a) ステータ3次

(b) ロータ3次

図5　D1モデル　磁束分布2

ポスト処理における周波数分解機能について，例を用いて紹介いたしました。
次数別の空間分布をみることで，目標値に向けた形状変更の手がかりが得られる可能性が示せたかと思います。ご使用いただければ幸いです。